我们之前学过数组的遍历、链表的遍历,这些线性结构的遍历考起来没有什么难度,可以理解为基本技能,一般也不会单独出题。
但是二叉树可不一样了,这一“开叉”,它的遍历难度陡然上了一个台阶。在面试中,二叉树的各种姿势的遍历,是非常容易作为独立命题点来考察的,而且这个考察的频率极高极高。 因此对于有志于在算法面试上求稳的同学,本节涉及的编码内容,你千万不要沉溺在“我看懂了”、“我理解了”、“我知道你说的是啥意思了”这种虚无的成就感中——假的,都是假的,只有自己写出来的代码才是真的!
理解只是记忆的前提,只吹理解不记忆,不如回家去种地:)。
这里我对大家的要求就是“在理解的基础上记忆”。如果你真的暂时理解不了,背也要先给你自己背下来,然后带着对正确思路的记忆,重新去看解析部分里的图文(尤其是图)、反复去理解,这么整下来你不可能学不会。 面试时见到二叉树的遍历,你不能再去想太多——没有那么多时间给你现场推理,这么熟悉的题目你没必要现场推理,你要做的是默写!默写啊!老哥们!!(捶胸顿足)
# 二叉树的遍历——命题思路解读
以一定的顺序规则,逐个访问二叉树的所有结点,这个过程就是二叉树的遍历。按照顺序规则的不同,遍历方式有以下四种:
- 先序遍历
- 中序遍历
- 后序遍历
- 层次遍历
按照实现方式的不同,遍历方式又可以分为以下两种:
- 递归遍历(先、中、后序遍历)
- 迭代遍历(层次遍历)
层次遍历的考察相对比较孤立,我们会把它放在后续的真题归纳解读环节来讲。这里我们重点要看的是先、中、后序遍历三兄弟——由于同时纠结了二叉树和“递归”两个大热命题点,又不属于“偏难怪”之流,遍历三兄弟一直是前端算法面试官们的心头好,考察热度经久不衰。
# 递归遍历初相见
编程语言中,函数Func(Type a,……)直接或间接调用函数本身,则该函数称为递归函数。
简单来说,当我们看到一个函数反复调用它自己的时候,递归就发生了。“递归”就意味着“反复”,像咱们之前对二叉树的定义,就可以理解为是一个递归式的定义:
- 它可以没有根结点,作为一棵空树存在
- 如果它不是空树,那么必须由根结点、左子树和右子树组成,且左右子树都是二叉树。
这个定义有着这样的内涵:如果我们想要创建一个二叉树结点作为根结点,那么它左侧的子结点和右侧的子结点也都必须符合二叉树结点的定义,这意味着我们要反复地执行“创建一个由数据域、左右子树组成的结点”这个动作,直到数据被分配完为止。
结合这个定义来看,每一棵二叉树都应该由这三部分组成:
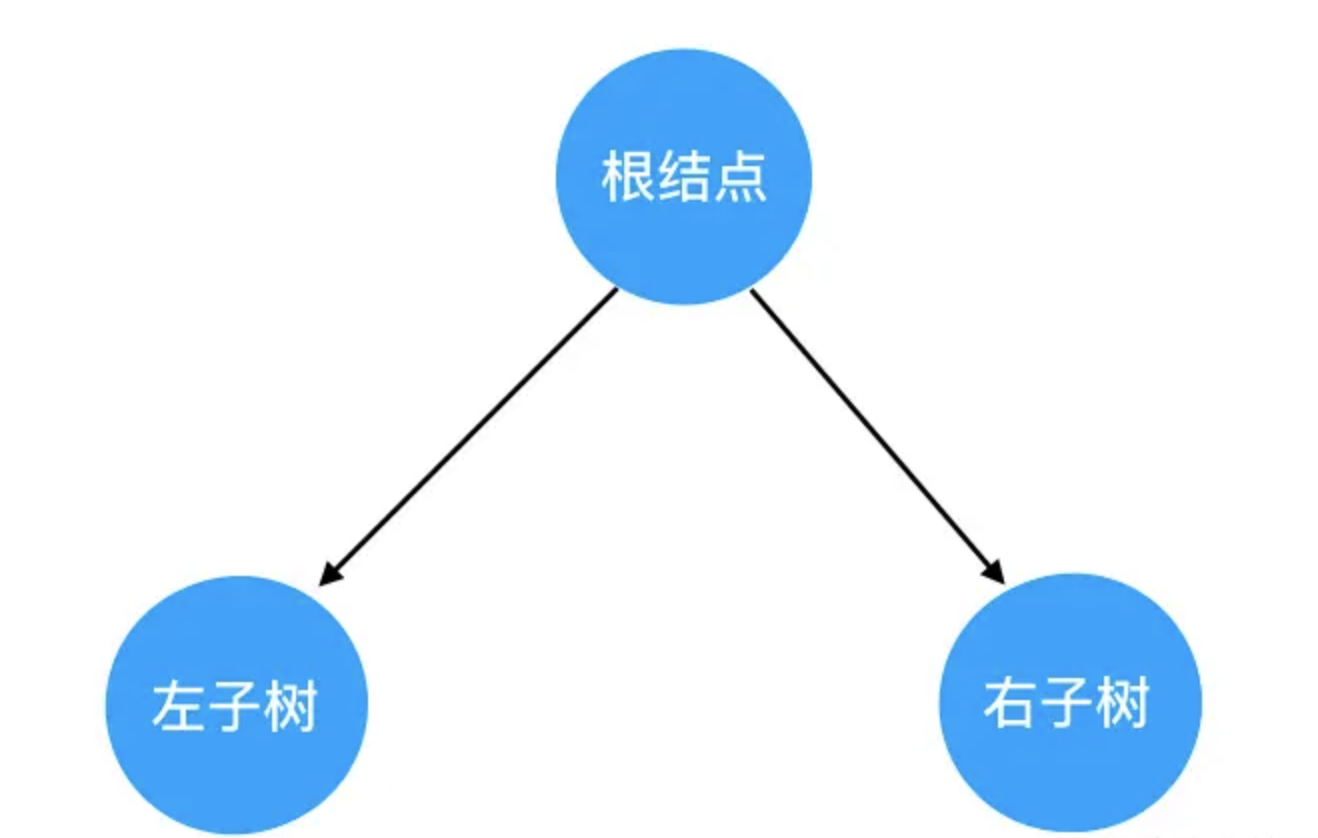
对树的遍历,就可以看做是对这三个部分的遍历。这里就引出一个问题:三个部分中,到底先遍历哪个、后遍历哪个呢?我们此处其实可以穷举一下,假如在保证“左子树一定先于右子树遍历”这个前提,那么遍历的可能顺序也不过三种:
- 根结点 -> 左子树 -> 右子树
- 左子树 -> 根结点 -> 右子树
- 左子树 -> 右子树 -> 根结点
上述三个遍历顺序,就分别对应了二叉树的先序遍历、中序遍历和后序遍历规则。
在这三种顺序中,根结点的遍历分别被安排在了首要位置、中间位置和最后位置。
所谓的“先序”、“中序”和“后序”,“先”、“中”、“后”其实就是指根结点的遍历时机。
# 遍历方法图解与编码实现
# 先序遍历
先序遍历的“旅行路线”如下图红色数字 所示:
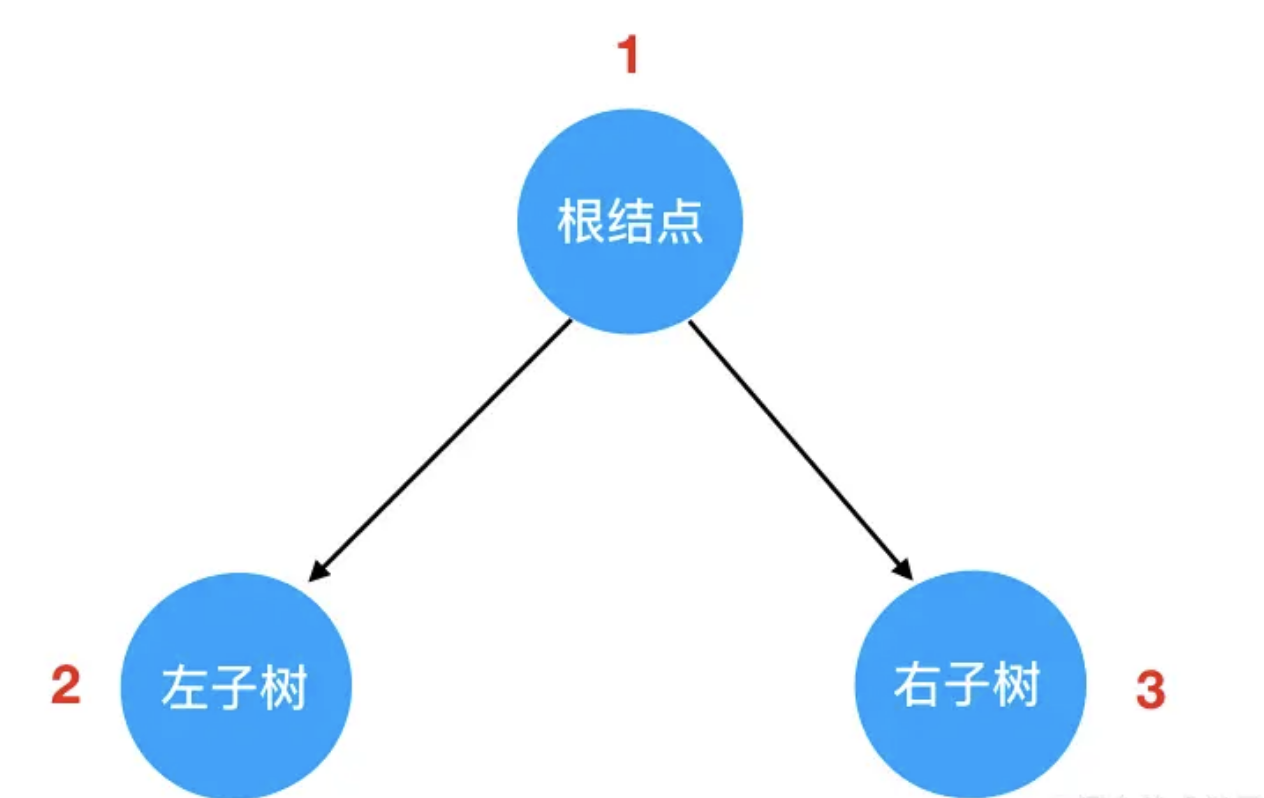
如果说有 N 多个子树,那么我们在每一棵子树内部,都要重复这个“旅行路线”,动画演示如下:
这个“重复”,我们就用递归来实现。
注:上面这个二叉树的结构,大家可以试着用我们前面学过的知识编码实现一把。这里为了方便大家理解,我直接给出来了哈(记得自己回去也要试着手写一遍):
const root = {
val: "A",
left: {
val: "B",
left: {
val: "D"
},
right: {
val: "E"
}
},
right: {
val: "C",
right: {
val: "F"
}
}
};
递归函数的编写要点
编写一个递归函数之前,大家首先要明确两样东西:
- 递归式
- 递归边界
递归式,它指的是你每一次重复的内容是什么。在这里,我们要做先序遍历,那么每一次重复的其实就是
根结点 -> 左子树 -> 右子树这个旅行路线。
递归边界,它指的是你什么时候停下来。
在遍历的场景下,当我们发现遍历的目标树为空的时候,就意味着旅途已达终点、需要画上句号了。这个“画句号”的方式,在编码实现里对应着一个 return 语句——这就是二叉树遍历的递归边界。
第一个递归遍历函数
上面咱们已经捋清楚思路,接下来话不多说,先序遍历的编码实现:
// 所有遍历函数的入参都是树的根结点对象
function preorder(root) {
// 递归边界,root 为空
if(!root) {
return
}
// 输出当前遍历