上一章给大家介绍了比例尺，它侧重于负责数据的映射，比如将数据映射为视觉元素的颜色、大小或者形状等属性。接下来会给大家介绍坐标系（Coordinate），它侧重于负责视觉元素的布局过程，将经过比例尺映射后的位置属性转换成画布坐标。

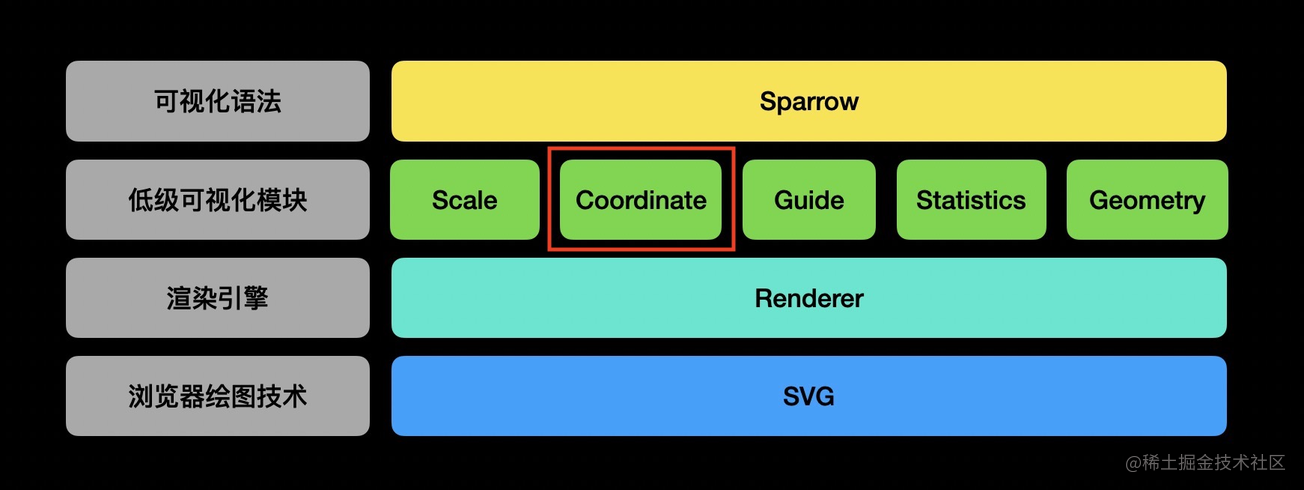
坐标系可以说是基于图形语法的图表库的一个独有的概念，它可以很方便的让图表在不同种类之间进行转换（比如从条形图转换成玫瑰图，堆叠条形图转换成饼图等等）。但是方便使用的同时，也带了实现上和理解的成本，所以希望大家看了这篇文章之后好好体会。

那么接下来我们将会从函数式编程讲起，因为 Coordinate 的开发和后续 Sparrow 的开发将依赖它。这之后再介绍坐标系理论以及实现方法，最后和前几章一样，进行简单的拓展。

# 函数式编程

我们首先进入函数式编程的学习。

相信大家都对面向对象编程这种编程模式（Object Oriented Programming，OOP）不陌生，毕竟很多人学习的第一门计算机编程语言可能就是 Java，而它就是一门典型的面相对象编程的语言。

这里将会给大家介绍另外一种编程模式：函数式编程（Funtional Programming, FP)。在这里介绍函数式编程的目的主要有两个：

• 函数式编程相对于面向对象编程会有一些优点（我们之后会看见），Sparrow 的代码的目标就是尽量拥有这些优点，让代码更加函数式。了解函数式编程可以让我们更好理解 Sparrow 的代码架构和选择。
• Coordinate 的实现依赖于函数式编程两个非常重要的工具。

我们首先会从一个例子简单来认识函数式编程，然后介绍其中两个重要概念：一等公民（First Class）和纯函数（Pure Function），最后介绍上面提到的两个工具：函数合成（Compose）和函数柯里化（Curry）。

# 计算海鸥数量

这里我们会用 Franklin Frisby 教授的 《Mostly Adequate Guide to Function Programming》 中的一个例子来初识函数式编程。

假如现有一个功能：计算多个海鸥群按照一定方式结合（Conjoin）和繁殖（Breed）后的海鸥总数。如果用面向对象的方式来实现该功能就如下：

// 定义一个海鸥群
// 这个群可以和别的海鸥群结合（Conjoin)和繁殖（Breed）
class Flock {
  constructor(n) {
    this.seagulls = n;
  }

  conjoin(other) {
    this.seagulls += other.seagulls;
    return this;
  }

  breed(other) {
    this.seagulls *= other.seagulls;
    return this;
  }
}

const flockA = new Flock(4);
const flockB = new Flock(2);
const flockC = new Flock(0);
const result = flockA
  .conjoin(flockC)
  .breed(flockB)
  .conjoin(flockA.breed(flockB))
  .seagulls; // 32

上面这段代码不仅让我们难以跟踪一直在变的内部状态（群体的海鸥数量），而且计算结果也是不正确的：最后的总数应该是16，flockA 的数量在结合和繁殖过程中被永远改变了。

那么接下来我们如何用函数式编程来实现相同的功能。

// add 相当于上面的 cojoin，multiply 相当于上面的 breed
// 这样命名的目的后面会讲
const add = (